Доказать, что $a$ является существенно особой точкой для функции \[ e^{\mathrm{tg}\,z},\quad a=\frac{\pi}{2} \] Закрываю дыры в доказательстве.
11.11.2023
06.11.2021
Задания и материалы для дистанционного занятия гр. 06-012 в 8:30 в сб. 6.11.2021 (Даишев, Кузнецова № 8.1 п.6; № 8.2 п. 3,4; 8.5 п.3; 8.11 п.2)
Изолированная особая точка функции – это точка, в которой функция не аналитична, но в любой окресности этой точки (кроме самой точки) - аналитична. Чем нам будут полезны изолированные особые точки (далее я их буду называть просто особыми точками) и что мы будем с ними делать - зависит от их разновидности.
02.11.2021
Задания и материалы для дистанционного занятия гр. 06-061 в 11:50 в вт. 2.11.2021 (Даишев, Кузнецова № 1.6 п.4, 2.11 п.4, 2.12 п.1)
Основы мы проходили в начале первого курса, так что начало объясню пунктирно.
30.10.2021
Задания и материалы для дистанционного занятия гр. 06-012 в 8:30 в сб. 30.10.2021 (Даишев, Кузнецова № 6.16, 7.1, 7.2, 7.13, 7.14)
Формула Коши была выведена в прошлый раз: \[ f\left(z_{0}\right)=\frac{1}{2\pi i}\oint\limits _{C}\frac{f\left(z\right)}{z-z_{0}}dz, \] где $f\left(z\right)$ – функция, аналитичная во всей области комплексной плоскости, ограниченной замкнутым контуром $C$, $z_{0}$ – точка из внутренности этой области.
02.11.2019
Даишев, Кузнецова №8.11 п.3 (вычет в бесконечности)
Вычет в бесконечности функции
\[
z^{3}\cos\frac{1}{z-2}
\]
равен, конечно, взятому с минусом вычету в двойке, который вычислялся тут и дал результат \( -\frac{143}{24} \). Но можно его вычислить и в лоб.
03.12.2017
Даишев, Кузнецова №8.32
Вычислить интеграл
\begin{equation}\label{main}
\int\limits_0^{\infty}\frac{x\sin x}{x^2+b^2}dx
\end{equation}
(предполагается, что $b\in \mathbb{R}$).
15.12.2016
Даишев, Кузнецова 9.5
Найти изображение
\[
\intop_{0}^{t}\frac{\mathrm{sh}\,\tau}{\tau}d\tau.
\]
Приведу оба решения, за которые вы взялись, но не доделали.
26.11.2013
Из домашнего задания гр.620а (по просьбе тов. Улахович)
Восстановить аналитическую функцию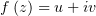 
, про которую известно,
что она:
1) Имеет мнимую часть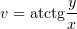 
,
2) Имеет известное значение в некоторой точке: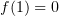 
.
08.11.2013
Ти ж мене пiдманула
Запутали вы меня, тов. Ханафиева и тов. Мубаракшин. Впрочем, я сам хорош, если вам это удалось.
12.10.2013
Восстановление дифференцируемой функции
Ещё одно пояснение для гр. 620а.
Условия Коши-Римана позволяют восстановить дифференцируемую функцию
по её действительной или мнимой части, если известно её значение в какой-либо
точке. Например, решить такую задачу:
(more…)
