Решения « Страница сетевой поддержки учеников Тимура Юрьевича Альпина

23.10.2011

Демидович №3991

Filed under: мат. ан. сем. 3 — Shine @ 2:03 пп

Найти площадь фигуры 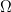$Ω$ , ограниченной графиком уравнения:

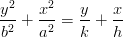2 2 y--+ x--= y-+ x- b2 a2 k h

(1)

перейдя к обобщённым полярным координатам.

(more…)

Comments (0)

Демидович №3988

Filed under: мат. ан. сем. 3 — Shine @ 1:59 пп

Найти площадь фигуры $Ω$ , ограниченной графиком уравнения:

( )2 y3 + x3 = y2 + x2

(1)

при $x > 0$ и $y > 0$ , перейдя к полярным координатам.

(more…)

Comments (0)

20.10.2011

13.10.2011

Пояснения к №34 из Даишева и Никитина

Filed under: ММФ — Shine @ 3:24 пп

Печатается по просьбе тов. Михеевой.
(more…)

Comments (0)

29.09.2011

Демидович, №3807

Filed under: мат. ан. сем. 3 — Shine @ 8:20 пп

Найти величину интеграла:

$\displaystyle I=\int\limits_{0}^{\infty }{e^{-x^2-\dfrac{a^2}{x^2}}\;dx}.$

(1)

(more…)

Comments (0)

13.09.2011

Даишев, Никитин №7

Filed under: ММФ — Shine @ 2:41 пп

Группа 692, в сабже при замене
delim{lbrace}{ matrix{2}{2}{ {s=} {y-cos(x)-x} {t=} {y-cos(x)+x} } }{}
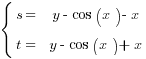
уравнение упрощается до формы 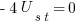$-4U_{s t}=0$ , если у вас получается что-то ещё — ищите ошибки.

Comments (0)

11.09.2011

Демидович, № 3726

Filed under: мат. ан. сем. 3 — Shine @ 9:56 пп

Доказать, что функция Бесселя \[ J_{n}\left(x\right)=\frac{1}{\pi}\intop_{0}^{\pi}\cos\left(n\varphi-x\sin\varphi\right)d\varphi,\quad n\in\mathbb{Z} \] удовлетворяет уравнению Бесселя \[ x^{2}J_{n}''\left(x\right)+xJ_{n}'\left(x\right)+\left(x^{2}-n^{2}\right)J_{n}\left(x\right)=0. \]

(more…)

Comments (0)

10.06.2011

Filed under: внешнее — Shine @ 3:04 дп

(more…)

Comments (0)

12.05.2011

Даишев, Кузнецова 8.32

Filed under: ТФКП — Shine @ 12:57 дп

Вычислить интеграл

$\displaystyle \int\limits_0^{\infty}\frac{x\sin x}{x^2+b^2}dx$

(1)

(предполагается, что $b\in \mathbb{R}$ ).

(more…)

Comments (0)

11.05.2011

Даишев, Кузнецова 7.10

Filed under: ТФКП — Shine @ 1:20 дп

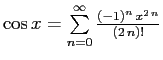Очевидно, что единственная кроме бесконечности особая точка функции $f(z)=z^3\,\cos\left(\frac{1}{z-2}\right)$ - это $z=2$ . Используя известное разложение косинуса $\cos x=\sum\limits_{n=0}^{\infty }{{\frac{\left(-1\right)^{n}\,x^{2\,n}}{ \left(2\,n\right)!}}}$ , представим функцию $f(z)$ так:

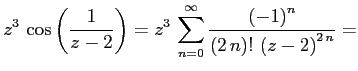
$\displaystyle z^3\,\cos \left({\frac{1}{z-2}}\right)= z^3\,\sum_{n=0}^{\infty }{ {\frac{\left(-1\right)^{n}}{\left(2\,n\right)!\,\left(z-2\right)^{2 \,n}}}}=$

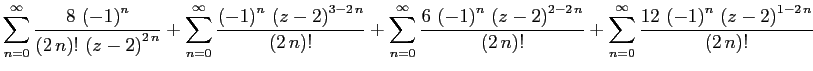
$\displaystyle \sum_{n=0}^{\infty }{{\frac{8\,\left(-1\right)^{n}}{\left(2\,n \... ...ac{12\,\left(-1 \right)^{n}\,\left(z-2\right)^{1-2\,n}}{\left(2\,n\right)!}}}$

Для того, чтобы найти вычет в точке $z=2$ , надо из этих сумм выбрать слагаемые, имеющие множитель $(z-2)^{-1}$ . Первая и третья из этих сумм содержат только слагаемые с целыми степенями $(z-2)$ , следовательно, нужные нам слагаемые есть только в этих суммах:

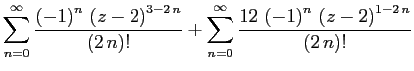
$\displaystyle \sum_{n=0}^{\infty }{{\frac{\left(-1 \right)^{n}\,\left(z-2\righ... ...ac{12\,\left(-1 \right)^{n}\,\left(z-2\right)^{1-2\,n}}{\left(2\,n\right)!}}}$

В первой сумме такое слагаемое соответствует $n=2$ , во второй - $n=1$ . Выпишем нужные слагаемые отдельно:

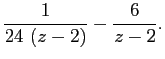
$\displaystyle {\frac{1}{24\,\left(z-2\right)}} -{\frac{6}{z-2}}.$

Если привести их к общему знаменателю, коеффициентом при $(z-2)^{-1}$ будет число $-\frac{143}{24}$ .

Comments (0)

« Newer Posts — Older Posts »